Ludwig von Bertalanffy

Hoy, hace 107 años, nace Karl Ludwig von Bertalanffy . El Padre de la Ingeniería de Sistemas.

Desde la biología planteó la idea de Sistemas abiertos (1950); concibió una explicación de la vida y la naturaleza como de un Sistema Complejo, sujeto a interacciones y dinámicas, que más tarde trasladó al análisis de la realidad social y a las estructuras organizadas bajo una descripción de amplio espectro que denominó TEORÍA GENERAL DE SISTEMAS, cuya exprersión definitiva, después de varios años de desarrollo apareció en el libro: General System theory (1969)

Fundó junto con otros importantes científicos con visiones sistémicas, la Society for General Systems Research (hoy ISSS).


RECURSOS:

Biografías: [1] [2] [3] [4] en alemán [5] en español

Ludwig von Bertalanffy (1901-1972): A Pioneer of General Systems Theory por Thaddus E. Weckowicz

Is Paul Weiss' and Ludwig von Bertalanffy's System Thinking still valid today? pManfred Drack y Wilfried Apfalter

Teoría de sistemas y sociedad por Tomás Austin Millán.

How von Bertalanffy’s critique of Marxist System Theory Self-Deconstructs por D. Boje

Fulfilling von Bertalanffy's Vision. The Synergism Hypothesis as a General Theory of Biological and Social Systems por Peter A. Corning

Cybernetics and Systems Thinkers

La teorización filosófica sobre la ciencia en el siglo XX por Pablo Lorenzano

El caos tiene su cuota de precisión

Tomado del diario Critica - Argentina

Sistema complejo. Las imágenes fractales son utilizadas para representar el caos en la naturaleza. Mindlin sostiene que el caos se aprecia en fenómenos cotidianos.

El físico Gabriel Mindlin y el escritor Gabriel García Márquez comparten algo más que el apodo familiar de “Gabo”: los dos escriben libros. Pero mientras el colombiano les da vida al pueblo de Macondo y a la dinastía de los Buendía, este investigador del Conicet y profesor de la Facultad de Ciencias Exactas y Naturales (UBA) se mete de lleno en una de las áreas más oscuras y pantanosas de las ciencias: el caos.

Sus encuentros y duelos con él están plasmados en Causas y azares: la historia del caos y los sistemas complejos (Siglo XXI), excusa y disparador de este diálogo en el que aclara e intriga: “El universo y la naturaleza son inherentemente caóticos. El ser humano, por más que incremente su tecnología y sus métodos de medición, no va a poder predecir todo”.

–Se suele hablar con mucha liviandad del caos: caos en la ciudad, caos en el tránsito, el mundo en caos, ¿no le parece?

–Demasiado. Evoca todo lo desorganizado, confuso, oscuro, incoherente. Aunque en realidad es algo matemáticamente preciso. En física se tardó un poco hasta dar con una palabra glamorosa y evocadora como la de “caos” para designar fenómenos donde no se puede predecir a largo plazo pese a que están regidos por leyes causales muy sencillas.

–¿Y por qué la eligieron?

–Porque a la comunidad científica le resultó atractiva. Fue como una operación de marketing. Pero la teoría del caos no explica el caos en el tránsito. Muchas veces uno tiene la idea de que por comprender ciertos fenómenos puede hacer extrapolaciones y predicciones. Y no es así en muchos sistemas. Muchas personas no conciben que a partir de reglas muy sencillas se pueden tener comportamientos muy complejos.

–¿Dónde se ve el caos?

–Se aprecia en fenómenos de todos los días, como fenómenos económicos, sociales, demográficos y epidemiológicos. Por ejemplo, la aparición de megacrisis a partir de pequeños cambios en las propiedades de ciertos agentes. El clima es un caso paradigmático. El universo en general está regido por fenómenos no lineales. Se dan a todas las escalas. En cualquier lugar donde pongas la lupa en la ciencia contemporánea hay chances de que encuentres propiedades no lineales. Es una teoría, ahora madura y sólida, que se va filtrando en diversas disciplinas.

–Y es muy antiintuitivo.

–Mucho. De alguna manera, el caos, la no linealidad y los sistemas complejos vienen a complicar un modo de pensar la ciencia que arranca con Newton. La naturaleza es intrínsecamente compleja.

–Y enigmática.

–Es cierto. Se sabe que, por un lado, están los fenómenos muy predecibles como los astronómicos. Dicen: va a haber un eclipse tal día, a tal hora, y ocurre. Pero no le creemos al que anuncia el estado del tiempo para este fin de semana.

–La ciencia se enorgullece de su capacidad predictiva.

–Tal cual. Es un mito que se derriba.

–Uno de los ejemplos más conocidos es el del “efecto mariposa”. ¿Es tan así como se dice?

–Es una metáfora nada más: dice que el aleteo de una mariposa en Hong Kong puede desatar un cataclismo en Nueva York. Es una exageración. Hay un ejemplo más lindo, el del cuento de Bradbury El ruido de un trueno, en el que un viajero del tiempo va al pasado, pisa una mariposa y al volver a su realidad hay pequeños cambios.

–Hay una parodia de Los Simpsons también.

–Si vos tenés un sistema donde tenés que elegir un camino y te obligan a volver a pasar por esas alternativas una y otra vez, lo que vas a tener es futuros totalmente distintos según las variaciones de las condiciones iniciales.

–Por eso elegir es siempre tan difícil. ¿Y cómo se investiga esto?

–Hay trabajo de escritorio, con computadoras y simulaciones numéricas, con matemática formal o experimentalmente. En mi caso, estudio el canto de las aves. Mi hipótesis es que los comportamientos complejos que se dan en las vocalizaciones y la comunicación animal están regidos por sistemas no lineales, con reglas muy simples. No es incompatible tener un pájaro que canta aleatoriamente a partir de una arquitectura neuronal sencilla.

La complejidad en el cerebro no es una necesidad para tener un canto y un comportamiento complejos. Esto se aplica a muchos campos: para explicar algo que es complejo no es necesario partir de un estado también complejo.

¿Qué es una red social en Internet?

...

Arquitectura de la Complejidad (parte III)

EVOLUCIÓN DE LAS REDES

La emergencia de estructuras de escala libre y de distribución de grado ley de potencias puede ser trazada bajo dos mecanismos. Estos mecanismos están ausentes de los clásicos modelos de grafos aleatorios, y más bien se presentan en varias redes complejas [11]. Primero, los modelos de la teoría de grafos tradicional asumen que el número de nodos en una red es fijo. En contraste, al WWW continuamente se expande añadiendo nuevos sitios web, mientras que la Internet crece con la instalación de nuevos routers, computadoras y vínculos de comunicación. Segundo, mientras que los modelos de grafos aleatorios asumen que los vínculos están aleatoriamente distribuidos, la mayoría de redes reales exhiben una preferencia adjunta. De hecho, es más probable que una persona enlace páginas web a documentos altamente conectados en la WWW, cuya existencia es harto conocida. Los motores de la red además tienden a conectar las computadoras de sus instituciones a través de nodos de gran ancho de banda, los cuales inevitablemente atraerán a otros consumidores y links.

Basados en el número creciente de nodos así como en la preferencia adjunta, se ha considerado un modelo simple en el cual un nuevo nodo es añadido a la red en cada instante de tiempo [11]. EL nuevo nodo luego es vinculado a alguno de los nodos ya existentes en el sistema (Figura 3). La probabilidad Π(k) que un nuevo nodo conecte a un nodo con k links sigue una regla de preferncia adjunta tal como:

Π(k)=k / (Σ ki) ... (2)

donde la suma es sobre todos los elementos de la red. Las simulaciones numéricas indican que la red resultante es de escala libre, y la probabilidad que un nodo tenga k vínculos viene (1) con exponente γ³ [11]. La naturaleza de la ley de potencias de la distribución es predicha por el enfoque basado en la ecuación de razón [19] así como de una solución exacta del modelo de escala libre [20]. Este simple modelo ilustra como el crecimiento y la preferencial adjunta conjuntamente llevan a la aparición de la jerarquía de hub que ejemplifican la estructura de escala libre. Un nodo con más links incrementa su conectividad más rápido que un nodo con menos links, debido a que el ingreso de nodos tiende a conectar a aquellos con mayor probabilidad tal como lo hemos descrito en (2). Este modelo conduce a un fenómeno de retroalimentación positivo de riqueza-a-ricos, el cual es evidente en algunos sistemas competitivos.

EL TALÓN DE AQUILES DEL INTERNET

Como la economía mundial ha vuelto crecientemente dependiente de Internet, surge una preocupación acerca de si la funcionalidad del Internet puede mantenerse aún bajo fallas y ataques hackers. Internet ha probado ser remarcadamente resilente contra fallos. Aunque alrededor del 3% de los routers están típicamente caídos en momentos particulares, nosotros raramente observamos disrupciones mayores en Internet. ¿Cómo Internet se puso tan robusta? Mientras significativa tolerancia al error se construyen en los protocolos que gobiernan las comunicaciones de “pasos de paquetes”, la topología de escala libre del Internet además juega un rol crucial en hacer esto más robusto.

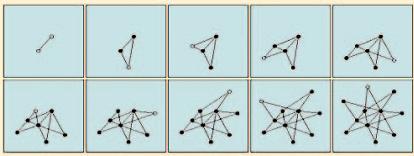
Figura 3 El nacimiento de una red de escala libre. La topología de escala libre es una consecuencia natural de la naturaleza expansiva de las redes reales. Comenzando de dos nodos conectados (arriba a la izquierda), en cada panel un nuevo nodo, el cual sem muestra como un punto abierto, es añadido a la red. Al decidir donde vincularse, nuevos nodos prefieren adjuntarse a los nodos más conectados. Gracias al crecimiento y a la adjunta preferencial, emergen unos pocos hubs altamente conectados. Después [1].

El concepto de percolación provee un enfoque para el entendimiento de la tolerancia al error inducida por la escala libre del Internet. La teoría de percolación especifica que la remoción aleatoria de nodos de una red da como resultado una transición de percolación inversa, cuando una fracción crítica fc de nodos es removida, los fragmentos de red sobrantes no comunican las islas de nodos. Sin embargo, simulaciones de redes de escala libre no apoyan las predicciones de la teoría de percolación [21]

Ver parte 1

Ver parte 2

Arquitectura de la Complejidad (parte II)

... viene de la parte I...

El propósito de este artículo es ilustrar, a través del ejemplo de la dinámica humana, que un entendimiento minucioso de un sistema complejo requiere un entendimiento de la dinámica de la red así como la topología y arquitectura de la red.

Luego de un panorama de la topología de las redes complejas tales como la Internet y la WWW, se dan los modelos generados por datos para dinámicas humanas. Estos modelos motivan el estudio de las dinámicas de las redes y sugieren que la teoría de la complejidad debe incorporar la interacción entre la dinámica y la estructura. El artículo además advierte la noción que un entendimiento de la dinámica de la red es facilitada por la disponibilidad de grandes conjuntos de datos y las herramientas de análisis venidas del estudio de la estructura de la red.

EL PARADIGMA DE LA RED ALEATORIA

Las redes complejas fueron inicialmente pensadas como si fueran completamente aleatorias. Este paradigma tiene sus raíces en los trabajos de Paul Erdös y Alfréd Rényi quienes, ayudando a describir las redes en comunicaciones y ciencias de la vida, sugirieron en 1959 que las redes se modelaran como grafos aleatorios [7], [8]. Este enfoque tomaba N nodos y los conectaba con L vínculos colocados aleatoriamente. La simplicidad del modelo y la elegancia de la teoría permitieron la emergencia de las redes aleatorias como un campo de estudio de las matemáticas [7]-[9].

Una predicción clave de la teoría de las redes aleatorias es que, a pesar de la posición aleatoria de los vínculos, la mayoría de nodos son asignados aproximadamente con el mismo número de vínculos. Ciertamente, en una red aleatoria los nodos siguen la distribución de campana de Poisson. Encontrar nodos que tienen un número significativamente grande o pequeño de vínculos en una elección aleatoria es por lo tanto raro. Las redes aleatorias son también conocidas como redes exponenciales porque la probabilidad de que un nodo esté conectado a otros k nodos decrementa exponencialmente por el tamaño de k (Figura 1). El modelo de Erös-Rényi, sin embargo, plantea la pregunta del si las redes observadas en la naturaleza son aleatorias. ¿Podría el Internet, por ejemplo, ofrecer servicio rápido y sin cortes si las computadoras estuvieran conectadas aleatoriamente unas con otras? ¿O podrías leer este artículo si los químicos en tu cuerpo repentinamente decidieran reaccionar aleatoriamente unos con otros sin pasar por la rígida red química que normalmente obedecen? Intuitivamente la respuesta es no, debido a que suponemos que detrás de cada sistema complejo hay una red subyacente con una topología no aleatoria. El reto del estudio de la estructura de redes, sin embargo, es escarbar en las señales de orden de la colección de millones de nodos y vínculos que forman una red compleja.

LA WORLD WIDE WEB Y LA INTERNET COMO REDES COMPLEJAS

La WWW contiene más de un billón de documentos (páginas web) los cuales representan los nodos de una red compleja. Estos documentos están conectados por un localizador de recursos uniforme (URLs), los cuales son usados para navegar de un documento a otro [Figura 2(a)]. Analizar las propiedades de la WWW, un mapa de cómo las páginas web están conectadas unas a otras se obtuvo en [10] usando un robot, o web crawler, el cual empezó desde una página web dada y recolectó las páginas a las cuales esta vinculaba (link). El robot luego siguió cada link de salida para visitar más páginas, recolectando sus respectivos links [10]. A través de este proceso iterativo una pequeña pero representativa fracción de la WWW puede ser mapeada.

Debido a que la WWW es una red direccionada cada documento está caracterizado por el número kout de sus links de salida, y el número kin de sus links de entrada. La distribución del grado de salida (entrada) por lo tanto representa la probabilidad P(k) de que una web seleccionada aleatoriamente tenga exactamente kout (kin) links. Además la teoría de grafos predice que P(k) sigue la distribución de la ley de potencias mostrada en la figura 2(c) y descrita por:

P(k) ~ k ^{– γ}, (1)

Donde γ_out ≈ 2.45 (γ_in ≈ 2.1).

Como lo ilustra la Figura 1, mayores diferencias topológicas existen en una red con una distribución de conectividad de Poisson y una con una distribución de conectividad de ley de potencias. De hecho la mayoría de los nodos en una red aleatoria unidireccional tienen aproximadamente el mismo número de links dados por k ≈ (k), donde el grado promedio. El decaimiento exponencial de la distribución de Poisson P(k) garantiza la ausencia de nodos con una significativa cantidad de nodos mayores que k y por ello impone una escala natural en la red. En cambio la distribución de ley de potencias implica que nodos con pocos links son abundantes mientras un pequeño número de nodos tienen abundantes links. Un mapa del sistema de carreteras de los EEUU, donde las ciudades son nodos y las autopistas son vínculos, ilustran una red exponencial. La mayoría de ciudades se ubican en la intersección de dos a cinco autopistas. Por otro lado, una red de escala libre es similar a los mapas de rutas de avión que se muestran en los folletos de vuelos. Mientras la mayoría de aeropuertos son alimentados por unos pocos transportistas, unos pocos hubs, tales como Chicago o Frankfurt, tienen enlaces a casi todos los aeropuertos en EEUU y Europa respectivamente. De este modo, al igual que los aeropuertos más pequeños, la mayoría de documentos WWW tienen un pequeño número de links, y , si bien estos links no son suficientes por sí mismos para garantizar que la red esté totalmente conectada, los pocos altamente conectados hubs garantizan que la WWW se mantenga unida.

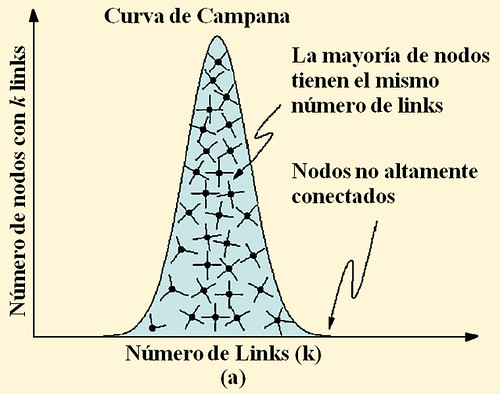
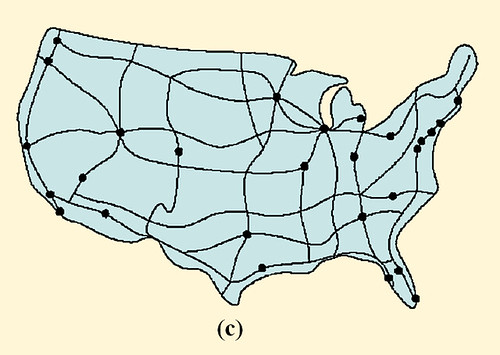
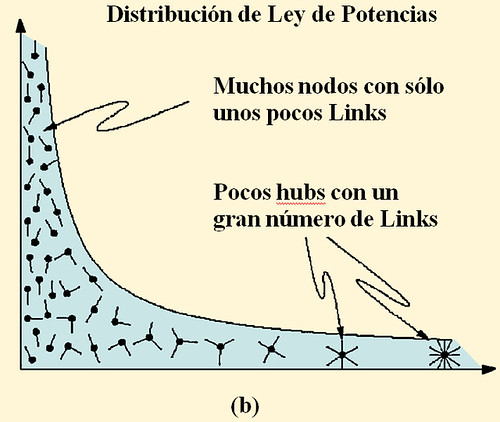
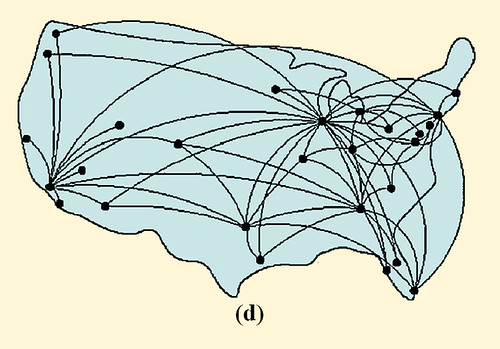
FIGURA 1 Redes Aleatorias y de escala libre. El grado de distribución de una red aleatoria sigue la distribución de Poisson cerrada con la forma de una curva de campana, diciéndonos que casi todos los nodos tienen el mismo número de links, y que los nodos con un gran número de links no existen (a). Esto es, una red aleatoria es similar a una red nacional de carreteras en las cuales los nodos son as ciudades y los vínculos son las mayores carreteras que las conectan. De hecho la mayoría de ciudades son conectadas por aproximadamente el mismo número de carreteras (c). en cambio la distribución de grado de ley de potencias de una red de escala libre predice que la mayoría de nodos tienen sólo unos pocos links que se mantienen juntos por muy pocos hubs altamente conectados (b). Tal red es similar al sistema de tráfico aéreo, en el cual un gran número de pequeños aeropuertos están conectados unos a otros mediante unos pocos hubs mayores (d). Luego [1]

A diferencia de la distribución de Poisson, una distribución de ley de potencias no posee una escala intrínseca, y su grado promedio no brida mucha información acerca de la estructura de la red. La ausencia de una escala intrínseca en k en redes con distribución de grado de ley de potencias motivo el concepto de red de escala libre [11]. Una red de escala libre es por lo tanto una red cuya distribución de grado obedece la ley de potencias. Mediciones empíricas, sin embargo, que las redes reales se desvían del comportamiento simple de la ley de potencias. La mayoría de desviaciones típicas están en la parte plana del grado de distribución en los pequeños valores de k, mientras la minoría de desviaciones típicas se encuentran en el corte exponencial para valores altos de k. Esto es, un ajuste apropiado para el grado de distribución de redes reales tiene la forma de P(k)=P(k+k0)^(-y) .exp(-k/kx), donde k0 es el grado más pequeño del corte y kx es la longitud de la escala del grado más alto del corte exponencial. El comportamiento de escala libre de las redes reales es por lo tanto evidente sólo entre k0 y kx .

La topología de escala libre de la WWW motiva la búsqueda de topologías no homogéneas en otros sistemas complejos tales como el Internet. Así como la WWW, el Internet es una red física cuyos nodos son routers y dominios y cuyos vínculos son líneas telefónicas y cables de fibra óptica que conectan los nodos [Figura 2(b)]. Debido a su naturaleza física, se espera que el Internet sea estructuralmente diferente a la WWW, dónde añadir un link arbitrariamente a una página web remota es tan fácil como linkear una página web en una computadora en la habitación del costado. La red Internet, sin embargo, además parece seguir el grado de distribución de ley de potencias como se observa en [12] [Ver Figura 2(b)]. En particular el grado de distribución mostrado sigue una ley de potencias con exponente y=2.5 para el router de la red, y y=2.2 para el mapa de dominio, lo cual indica que el cableado del Internet está además dominado por muchos hubs altamente conectados [12].

19 Grados de Separación
Stanley Milgram mostró empíricamente en 1967 que dos personas cualesquiera están de 5 a seis “apretones de mano” alejados uno del otro. [13]. Esto es, la mayoría de humanos en la tierra parecen vivir en un pequeño mundo. Esta característica de las redes sociales es conocida como propiedad de los seis grados de separación (six-degrees of separation) [14]. Además los sociólogos sostienen repetidamente que los nodos en las redes sociales están agrupados en pequeños clusters. Estos clusters representan círculos de amigos y conocidos, y dentro de cada cluster un nodo está conectado a todos los otros nodos pero tiene sólo escasos vínculo con el mundo exterior [15]. La pregunta que surge es si el modelo del mundo pequeño es aplicable a la WWW y al Internet.

Debido a que no hay disponible un mapa completo de la WWW [16], se usan pequeños modelos de computadora de la WWW en [10], donde la distribución del vínculo coincide con la forma de medición funcional y donde las distancias más cortas entre cualesquiera dos nodos son identificados y promediados para todos los pares de nodos para obtener la separación promedio de nodos d. Repitiendo este proceso para redes de diferentes tamaños usando escalamiento de tamaño finito, un procedimiento estándar en mecánica estadística, se infiere en [10] que d=0.35+2.06.Log(N), donde N es el número de nodos de la WWW. Para los 800 millones de nodos de la WWW en 1999, el típico camino más corto entre dos páginas web aleatoriamente seleccionadas es pues alrededor de 19, asumiendo que cada camino existe, lo cual no está siempre garantizado debido a la naturaleza direccionada de la web. Como se muestra de forma empírica en [17], sin embargo, para 200 millones de nodos esta distancia es 16, en contraste con los 17 predichos en [10].

Estos resultados indican que la WWW representa un pequeño mundo y que el número típico de clicks entre dos páginas web es alrededor de 19, a pesar del número actual de más de 1 billón de páginas web. Además, la WWW muestra un alto grado de clustering [18], esto es, la probabilidad que dos vecinos de un nodo dado estén también linkeados es mucho mayor que el valor esperado para una red aleatoria. Finalmente, los resultados del reporte en [1] indican que el Internet además posee una estructura de pequeño mundo.

Dinámica de Sistemas : Casos y Aplicaciones para América Latina

El Capítulo Latinoamericano de la Sociedad de Dinámica de Sistemas después de varios meses de trabajo virtual ha terminado finalmente de elaborar el libro : Dinámica de Sistemas : Casos y Aplicaciones para América Latina, cuya edición estuvo a cargo de Isaac Dyner y Luisa Rodríguez.

Libro completo -->>>> DESCARGAR

Contenido


Prólogo
Isaac Dyner y Luisa Rodríguez


PARTE I: Pedagogía de la Dinámica de Sistemas

1. Introducción al Pensamiento Sistémico. Pensamiento sistémico, un nuevo paradigma
Angélica Martínez

2. Herramientas para la enseñanza de la Dinámica de Sistemas
Samuel Prieto

3. Didácticas en la enseñanza de Dinámica de Sistemas
Martín Schaffernicht

4. "Prosa" sistémica y dinámica como elemento de sensibilización y de cambio de enfoque
Fabián Szulanski

5. Experimentos de laboratorio en Dinámica de Sistemas
Santiago Arango y Erling Moxnes

6. Propuesta para la difusión de la Dinámica de Sistemas en la escuela
Hugo Andrade y Ximena Vargas


PARTE II: Aplicaciones en educación

7. Gestión universitaria con Dinámica de Sistemas
Lilia Gélvez

8. Dinámica de Sistemas en la medición del emprendimiento
Luisa Rodríguez

9. Dinámica de Sistemas y aprendizaje en contaduría: Una experiencia en el aula.
Jorge Juliao y Ómar Díaz

10.Workshop. Simulador de carrera laboral
Eduardo Fracassi


PARTE III: Aplicaciones en política pública

11. Modelo en Dinámica de Sistemas para gestión socio ambiental
Mauricio Díaz

12. Micromundos en la comercialización de energía en ENERBIZ
Santiago Arango, Isaac Dyner y Carlos Franco

13.Sistema integrado de vigilancia y control de malaria y dengue en Colombia
Daniel Ruiz Carrascal, Stephen Connor y Madeleine Thomson

14. Modelo de gerencia sistémica de activos y pasivos en fondos de pensiones.
Ricardo Matos

15.Tras las estructuras del crimen y la justicia
Sebastián Jaén e Isaac Dyner


PARTE IV: Aplicaciones en estrategia empresarial

16. Cómo hacer estrategia usando Dinámica de Sistemas
Martín Kunc

17. FODA dinámico."Reporte de una página" dinámico
Fabián Szulanski

Arquitectura de la Complejidad (parte I)

Artículo de Albert-László Barabási. Pueden encontrar el original (en inglés) AQUÍ .

Estamos rodeados por Sistemas Complejos, desde células hechas por miles de moléculas hasta sociedades, una colección de millones de interacciones individuales. Estos sistemas exhiben señales de orden y auto-organización. El entendimiento y cuantificación de esta complejidad es un gran reto para la ciencia. La teoría cinética, desarrollada a finales del siglo XIX, muestra que las propiedades medibles de los gases, desde la presión hasta la temperatura, pueden ser reducidos al movimiento aleatorio de átomos y moléculas. En los 60's y 70's, investigadores desarrollaron enfoques sistemáticos para cuantificar la transición de desorden a orden en sistemas materiales tales como magnetos y líquidos. La Teoría del Caos dominó la búsqueda por entender el comportamiento complejo en los 80's con el mensaje que el comportamiento impredecible puede emerger de las interacciones no lineales de unos pocos componentes. Los 90's fue la década de los fractales, cuantificando la geometría de los patrones emergentes en sistemas auto-organizados, desde hojas hasta copos de nieve.

A pesar de estos avances conceptuales, no existe aún una teoría de la complejidad completa. Cuando intentamos caracterizar Sistemas Complejos, las herramientas de que disponemos fallan por diversas razones. Primero, los sistemas complejos no están hechos de componentes idénticos tales como los gases y los magnetos. Aún más, cada gen en una célula o cada individuo en una sociedad tiene su propio comportamiento característico. Segundo, mientras que las interacciones entre los componentes son manifiestamente no lineales, verdaderamente el comportamiento caótico es más la excepción que la regla. Tercero, y más importante, las moléculas y las personas no obedecen ni al desorden extremo de los gases, donde cualquier molécula puede colisionar con otra, o al orden extremo de los magnetos, donde los spins interactúan sólo con su vecindad inmediata en una rejilla periódica. Es más, en sistemas complejos, las interacciones forman REDES, donde cada nodo interactúa con sólo una pequeña cantidad de parejas seleccionadas cuyas presencias y efectos pueden ser sentidos en nodos muy lejanos.

Las redes exisen en todos los lugares y en todas las escalas. el cerebro es una red de células nerviosas conectadas por axons, mientras que las células son redes de moléculas conectadas por reacciones bioquímicas. Las sociedades, también, son redes de personas vinculadas por amistad, familia, y lazos profesionales. A una gran escala, redes de alimentos y ecosistemas se pueden representar como redes de especies. Por otro lado, las redes invaden la tecnología; como ejemplos tenemos la Internet, redes de energía eléctrica y los sistemas de transportes. Aún el lenguaje usado para transmitir pensamientos es una red de palabras conectadas por relaciones sintácticas.

A pesar de la pervasividad de las redes, sin embargo, su estructura y propiedades aún no son totalmente entendidas. Por ejemplo, los mecanismos mediante los cuales genes disfuncionales en una red genética compleja llevan a la producción del cáncer no es obvia, y la difusión rápida a través de redes sociales y de comunicación que llevan alas epidemias de enfermedades y los virus de computadotas aún no son bien caracterizados. Además, es importante entender cómo algunas redes continúan funcionando a pesar de fallas en la mayoría de sus nodos.

Investigaciones recientes están empezando a responder tales preguntas [1]-[6]. Hace unos pocos años los científicos han descubierto que las redes complejas tienen una arquitectura subyacente guiada po prinipios universales. Por ejemplo, muchas redes, desde la world wide web (www), los sistemas metabólicos de las células, hasta los actores de Hollywood, son dominados por un pequeño número de nodos que están altamente conectados a otros nodos. Estos nodos importantes llamados hubs, afectan en gran medida el comportamiento total de las redes. Como describimos en este artículo, os hubs hacen a las redes robustas contra fallas accidentales pero vulnerables a ataques coordinados.

(continua...)

¿Qué es una Red?

Tomado de NECSI (por Yaneer Bar-Yam) (versión original, en inglés aquí)

Una red es una descripción de las conexiones que permiten las interacciones e influencias entre las partes de un sistema complejo. Además se usa para referirse a las partes junto con su conexiones, i.e. los sistemas como totalidad, cuando consideramos los efectos de esas conexiones.

Hay varios tipos de redes:

redes de transporte - las carreteras de una ciudad,
redes de comunicación - la red telefónica,
redes de servicio público - la malla de potencia eléctrica de un país.
redes de abastecimiento - el sistema de abastecimiento de alimentos en una ciudad,
redes de reacciones moleculares - redes metabólicas,
redes de células - redes neuronales,
redes de computadoras - internet, y
redes sociales - la gente en una empresa, o en una comunidad.

Una propiedad importante de las redes es su topología: i.e. cuáles elementos están directamente relacionados con cuáles otros. Entonces , pueden discutirse propiedades más específicas de las conexiones. Cada conexión de lared puede ser caracterizada por propiedades tales como su rango de influencia, capacidad, etc.

Todas las redes pueden ser pensadas como redes de influencia: el estado de las partes que están conectadas a una red afectan a los otros a través de la red. Conceptualmente podemos distinguir entre redes que transfieren materiales (abastecimiento, transporte, servicios públicos, químicos), y redes que transfieren información (neuronas, comunicación, computadoras, sociales).

La manera en que pensamos las redes a menudo depende de cuan complejo sea el comportamiento de la red misma. Por ejemplo, a menudo pensamos en el sistema de transporte como una red en sí misma, a pesar que es una red que se conecta al sistema socioeconómico. En este caso pensamos en los atascos de tráfico y no acerca del rol de las carreteras como conectores. En otros casos nosotros nos enfocamos en cómo se comportan las partes como resultado de sus conexiones a través de la red, o cómo el sistema, como un todo, se comporta debido a las partes de la red.

En muchas de las redes más comúnmente estudiadas se asume que éstas están conectadas a partes similares, con conexiones que son en cierto sentido similares. Por lo tanto la atención se centra sólo en la topología de la red que caracteriza este comportamiento. Sin ebargo, de modo más general, las redes reales conectan partes disímiles en distintos modos.

Como parte del estudio de sistemas complejos, el entendimiento general que nosotros obtenenos de como se comportan las redes puede ser transferido entre varios tipos de sistemas, si son físicos, biológicos, sociales o de ingeniería. Es útil pensar acerca de los comportamientos que son comunes a diferentes tipos de redes, y los que son diferentes.

SISTEMAS DINÁMICOS Y MODELOS BASADOS EN AGENTES

En el estudio de sistemas socio-económicos complejos, cuando uno se enfrenta a la decisión de elegir el modelo de simulación, se debe tener en cuenta las características del sistema que le interesan modelar, por la esencia misma de los sistemas estos tienen múltiple naturaleza (como la naturaleza corpuscular y ondulatoria de la luz). Siendo éstas complementarias.

En la literatura podemos encontrar claramente diferenciados dos tipos importantes de Modelos:

• Modelos Dinámicos, que capturan el comportamiento del sistema como agregado de totalidades, distribuciones de atributos para subpoblaciones de un sistema; la metodología de modelamiento más usada es la Dinámica de Sistemas, que con niveles y flujos, describe el comportamiento en el tiempo de partes que interactúan de modo no lineal, y con bucles de retroalimentación.

Aqui por ejemplo el subsistema construcción de un modelo hecho con el software para Dinámica de Sistemas: Stella, de un sistema que intenta capturar la dinámica poblacional de la ciudad de Cajamarca (Perú).

• Modelos Basados en Agentes, observa las consecuncias globales da la simulación de las decisiones, percepciones y acciones de individuos interactuando en un espacio dado; se trata de simular numerosos agentes heterogeneos, lo que s eobserva es el resultado de las interacciones entre ellos.

Aqui la simulación con el software Netlogo de un modelo que intenta simular el fenómeno de segregación.

Ambos modos capturan distinta características de los sistemas, se pudieran usar de modo complementario.


Existe además otros modos de visualizar sistemas complejos con teoría de redes por ejemplo.

Para más detalles revisar:

• "Teorías de la Complejidad y el Caos en Ciencias Sociales. Modelos Basados en Agentes y Sociedades Artificiales", Jorge E. Miceli - Sergio G. Guerrero - Ramón A. Quinteros - Diego Díaz - Mariano Jordan Kristoff – Mora Castro (en pdf - bajar aqui)

• International Network for Social Network Analysis (website)

• Modelos basados en agentes (wikipedia)
  

• Curso de Netlogo, en español, (entrar como invitado, link aqui)

• Software para simulación (Sistemas basados en agentes y Dinámica de Sistemas) Netlogo

• System Dynamic Society (website)

• Software para simulación de redes Network Workbench (website)

• Tutoriales de Network Workbench (website)

• Capítulo Latinoamericano de la Sociedad de Dinámica de Sistemas (website)

• Cacit group - Dinámica de Sistemas (website)
  

Principios de la Ingeniería de Sistemas

Tomado de : http://sunwc.cepade.es/%7Ejrivera/org_temas/org_praxis/estructuras/s_e_estructura_org.htm

Principios fundamentales a seguir en la Ingeniería de Sistemas (IS):

Observación, consideración "holística"

La IS, es metodología "holística" (del griego, "holos"=todo): debe estructurar el tratamiento racional de proble­mas, o de los métodos para su solución, de tal forma que se tengan en cuenta "todos" los factores influyentes en la situación de problema.

En general, un enfoque de la IS difiere del tratamiento convencional de problemas en cuanto a su "generalidad", en su base lógica o mental, y en su búsqueda de los principios o factores más universales que puedan haber contribuído a provocar la situación-problema analizada.

Autopoiesis de los sistemas

La SE, como la Teoría general de Sistemas, parte del principio de que un sistema es construido como autocon­figurado y autodelimitado frente a su entorno, por "reducción selectiva de complejidad" conseguida desde el mismo sistema, y mantenida en su permanente auto-referencia y auto-reproducción ("autopoiesis").

El grado de complejidad de un sistema es siempre menor que el de su entorno. Esa complejidad se concreta en las relaciones entre las áreas de problemas, una empresa, p.ej., la reduce al seleccionar un segmento de mercado con determinadas necesidades a satisfacer.

Aprendizaje/Evolución

En el marco de la actividad empresarial de “creación de valor”, la INNOVACIÓN constituye quizá la actividad más importante (la que según Schumpeter constituía realmente la característica distintiva del Empresario-Emprendedor). Ahora bien, en la evolución del planteamiento de la ingeniería de sistemas era lógico que al querer extenderla a nuevos campos de trabajo hubiera que plantearse el tema de la innovación (en el dominio estudiado, es decir, en el campo de objetos) y el tema del aprendizaje del equipo o sistema-activo que realiza la configuración o ingeniería del sistema-solución.

El modelo básico de la “máquina cibernética” (como “máquina trivial”) era realmente inadecuado pues el “regulador” con las magnitudes-meta que sirven para controlar los flujos de inputs desde la medición del flujo de outputs es independiente de la situación del entorno. Por eso es preciso pasar a un modelo de “doble bucle” en que esas mismas magnitudes de control sean modulables según el entorno y los mismos inputs. Von Foerster utilizó el modelo de la “máquina de Turing” para desarrollar su “máquina no trivial” en que los outputs (soluciones a los problemas planteados) no sólo serán ya resultado de la “transformación” de inputs en un primer circuito cibernético, sino también dependerán de que las magnitudes de control de ese primer sistema productor de solucioines sea modulado por un segundo sistema (el sistema observador) inserto también en el mismo entorno y sometido a los mismos flujos de inputs. Ese sistema superior (sistema observador y activo) deberá pues ser capaz de “aprender”, es decir, ser capaz de manejar nuevas magnitudes (en orden a definir nuevos objetivos y metas, y también nuevos criterios o magnitudes de control). Los outputs de este sistema superior – que han de ser los que controlen el sistema-objeto en configuración – se configuran pues como resultado de su actividad (resultante de haber “aprendido”), una actividad que – en forma paralela a la de la configuración del sistema-objeto a la que denominamos “ingeniería” – se denomina “imaginería” (“Imagineering”).

El término debe formular la idea de que el proceso de la configuración del futuro (del sistema-objeto solución) implica un “des-aprender” contenidos tradicionales, y un “aprender” creativo de nuevos conceptos etc. (Hamel/Prahalad 1994 [1]).

El sistema activo no puede permanecer anclado en una estructura fija, sino él mismo deberá evolucionar “aprendiendo” en interacción continua con el campo de problemas analizado en que se configura (en ingeniería activa) el sistema solución. Tal aprendizaje deberá concentrarse en las competencias clave (¡Gestión del conocimiento!).

Temporalidad: principio de la consideración dinámica- evolucionista

Se trata de no olvidar la dimensión temporal, y de flujo de las situacio­nes-problema. La IS impone como principio metodológico no restringir la consideración de ningún problema al punto temporal del presente, es decir, superar la visión estaticista para llegar a ver toda situación problema en su dimensión de flujo temporal.

La IS considera los sistemas-objeto como algo dinámico, como algo donde ocurren eventos. El "modelo" construído en el sistema-configurador tendrá que poder representar al sistema-objeto como secuencia de estados distintos en dependencia del tiempo. La variabilidad temporal del sistema se refiere a:

- los tipos e intensidades de las relaciones entre el sistema y el entorno

- los tipos e intensidades de las relaciones en el interior del sistema

- las mismas propiedades de los elementos del sistema

- la misma estructura u ordenamiento mutuo de los elementos del sistema.

Sólo en esta apertura a lo nuevo se crea la base para realizar una ingeniería de sistemas que incluso cree mercados futuros.

Principio de la estructuración (jerárquica o en redes) de sistemas:

La IS, como la Teoría de Sistemas, parte del supuesto de que la mayoría de los sistemas se configuran en su tratamiento y reducción de la complejidad mediante la "interpenetración" de subsistemas (antes se hablaba de "partes") que a su vez reducen externa a ellos y crean complejidad interna. En atención a la estructuración interna del sistema-2 (sistema-objeto) en subsistemas, y en atención a las capacidades del subsistema cognitivo, la IS propone que todo método de solución de problemas complejos realice una división (análisis) de la temática a estudiar, y que la estructure (síntesis).

Este trabajo debe realizarse por diferenciación progresiva, por aumento del grado de detalle en el estudio de los objetos tratados.

Aunque el trabajo de estructuración tradicionalmente siguió el procedimiento de desglose "jerárquico" (por ejemplo, en estructuras arborescentes, como el árbol de funciones en el primer Value Analysis), hoy se trabaja en desgloses en "networks" (la técnica del "hypertext", por ejemplo) que además mantienen entre sus nudos relaciones no deterministas (según el concepto lógico de los conjuntos difusos - fuzzy sets).

Exigencia de la "reducción de complejidad"

La metodología de la IS impone "delimitar" - por diferencia frente al entorno - el ámbito del problema a elaborar. Esa delimitación implica dejar fuera del campo de estudio ciertos aspectos, los considerados menos relevantes, y destacar otros factores. Se pide a los métodos concretos que ayuden a realizar esta selección: p.ej. como en el Pareto, o ABC. Asimismo se pide distingan síntomas aparentes de causas o factores profundos. También se debe delimitar el campo de lo "factible" frente al de lo "utópico". En esta delimitación se pide se cumpla la racionalidad de la "aurea mediocritas" (evitar la "hybris" o el exceso): hasta el mismo cumplimiento excesivo de la norma jurídica puede llevar a vulnerar la norma de justicia ("summum ius, summa iniuria" - máxima legalidad, máxima injusticia).

Diferenciar entre Sistema Configurador y Sistema Objeto

La metodología normativa de la solución de problemas en la IS exige la constitución de un "sistema-configurador" o sistema-acción (que abarque la situación concreta y sus entornos, incluyendo el o los sujetos encargados del tratamiento de problemas. Un ejemplo de tal creación de sistema de solución de problemas con­siderados desde un enfoque común se encuentra en la formación de un "proyecto" (de AV, etc.) o en la creación de una "transfunción" como la del "Controlling" o la "Logística". Crear un sistema implica trazar sus límites frente al entorno.

La metodología de la IS impone además delimitar - por diferencia frente al entorno - el ámbito del problema a elaborar. Esa delimitación implica dejar fuera del campo de estudio ciertos aspectos, los considerados menos relevantes, y destacar otros factores. Se pide a los métodos concretos que ayuden a realizar esta selección: p.ej. como en el Pareto, o ABC. Asimismo se pide distingan síntomas aparentes de causas o factores profundos. También se debe delimitar el campo de lo "factible" frente al de lo "utópico". En esta delimitación se pide se cumpla la racionalidad de la "aurea mediocritas" (evitar la "hybris" o el exceso): hasta el mismo cumplimiento excesivo de la norma jurídica puede llevar a vulnerar la norma de justicia ("summum ius, summa iniuria" - máxima legalidad, máxima injusticia).

---

[1] Hamel G./Prahalad, C.K. (1994): Competing for the Future. Boston.

Los sistemas auto-organizados y la ingeniería de sistemas...

Francisco Maturana en el prefacio a la edición de 1994 de "De Máquinas y Seres Vivos" menciona lo siguiente:

[... un sistema, cualquiera sea este, surge en el momento en que en un conjunto de elementos comienza a conservarse una dinámica de interacciones y de relaciones que dan origen a un clivaje operacional que separa a un subconjunto de esos elementos que pasa a ser un sistema, de otro elementos que quedan excluidos de éste y que pasan a ser el entorno. La dinámica de interacciones y relaciones que como configuración relacional entre elementos al conservarse separa a un conjunto de elementos de otros dando origen a un sistema, pasa a ser la organización del sistema, en tanto que el conjunto de elementos y relaciones que realizan esta organización en la unidad operacional que surge así separada de un medio como un ente particular, pasa a ser la estructura.]

Francis Heylighen, por otro lado, en su muy leído artículo "The Science of Self-organization and Adaptivity", menciona con mucho acierto esto:

El cibernetista británico W. Ross Ashby propuso lo que llamó “el principio de autoorganización”. El notó que un sistema dinámico, independientemente de su tipo o composición, siempre tendía a evolucionar hacia un estado de equilibrio, o lo que podríamos ahora llamar un atractor. Esto reduce la incertidumbre que tenemos acerca del estado de sistema, y por consiguiente la entropía estadística del sistema. Esto es equivalente a la auto-organización. El equilibrio resultante puede ser interpretado como un estado donde las diferentes partes de sistema están mutuamente adaptadas.

La auto-organización es básicamente la creación espontánea de patrones coherentes globalmente provenientes de interacciones entre componentes inicialmente independientes. Este orden colectivo está organizado en función de su propio mantenimiento, y de este modo tender a resistir perturbaciones. Esta robustez se logra con el control distribuido y redundante de modo que cualquier daño pueda ser restaurado por las secciones restantes no dañadas.

El mecanismo básico subyacente a la auto-organización es la variación determinista o estocástica que gobierna cualquier sistema dinámico, explorando diferentes regiones en el espacio de estados hasta que cae en un atractor, i.e. a una configuración que se cierra en sí misma. Este proceso puede ser acelerado y profundizado por el incremento de variación, por ejemplo por adición de “ruido” al sistema. La entrada a un atractor impide futuras variaciones fuera del atractor, y por lo tanto, restringe la libertad de los componentes del sistema de comportarse independientemente. Esto es equivalente al incremento de coherencia, o disminución de la entropía estadística, que define la auto-organización.

La clausura define al sistema separado de su entorno, definiéndolo como autónomo. La clausura usualmente es el resultado de la naturaleza retroalimentada y no lineal de las interacciones. Si la retroalimentación es positiva llevará a un crecimiento explosivo de cualquier configuración originalmente que entra en el régimen de retroalimentación positiva. Este crecimiento acaba cuando todos los componentes disponibles han sido absorbidos en una nueva configuración, dejando al sistema en un estable estado de retroalimentación negativa.

La teoría de auto-organización tiene muchas aplicaciones potenciales -pero aún relativamente poco prácticas- En principio ofrece una visión del funcionamiento de la mayoría de sistemas complejos que nos rodean, desde galaxias y planetas hasta moléculas, y desde células vivas a ecosistemas y mercados. Tal entendimiento sin embargo no necesariamente lleva a una mejor capacidad de predicción, debido a que el comportamiento de los sistemas auto-organizados es impredecible por su propia naturaleza. Por otro lado, obtener una mejor comprensión de las fuentes relevantes de selección, la variación y las estructuras intrínsecas de un atractor nos ayudarán a conocer cuáles comportamientos son posibles y cuáles son imposibles.

Los sistemas complejos han llamado la atención de físicos, biólogos, eologistas, economistas y científicos sociales. Las ideas sobre sistemas complejos están abriendo caminos en antropología, ciencias políticas y finanzas. Muchos ejemplos de redes complejas que tienen un gran impacto en nuestras vidas -tales como supercarreteras, electrificación e internet- vienen de la ingeniería. Pero, aunque los ingenieros pueden haber desarrollado los componentes, ellos no han planeado su conexión.

Las principales características de los sistemas complejos son la auto-organización, la adaptación y la emergencia. En el estudio y entendimiento de lo sistemas complejos radica el corazón de la Ingeniería de Sistemas; y el trabajo trnadisciplinario es básico en la búsqueda de hacer ciencia y buscar un mejor entendimiento de la realidad compleja que nos rodea.

Teoría del Caos y Ciencias Sociales

Mapa de bifurcación 4-dimensional

Hace poco leí un ensayo muy interesante, escrito ya hace mucho, titulado "CHAOS THEORY AND POSTMODERN PHILOSOPHY OF SCIENCE,DE NOVUM ORGANUM,The New Body of Scientific Knowledge" , escrito por T.R. Young.

Hay todo un movimiento que trabaja en las implicaciones de la Teoría del Caos en las Ciencias Sociales, y está teniendo grandes avances...

Aquí un extracto de ese ensayo:

La Teoría del Caos es una manera resumida de hablar sobre la dinámica no lineal de la mayoría de sistemas naturales y sociales que encontramos en el mundo real. Algunos de los que trabajan en este campo hablan de ciencia de la complejidad; otros hablan de teoría de la bifurcación, fractales, o, simplemente, no linealidad. Todas ellas relacionadas con los patrones, las regularidades y las certezas que se encuentran en los mismos campos de resultados en los cuales se encuentran también el desorden, la incertidumbre, y las transformaciones inesperadas. Se trata de un viaje difícil con muchas verdades sin descubrir y poco hechos inmutables. La Teoría del Caos es el estudio de las relaciones cambiantes entre el orden y el desorden. (Briggs and Peat, 1988; Gleick, 1988; Holden, 1986; Mandelbrot, 1977).

La Teoría del Caos motiva una ciencia postmoderna que es impredecible, por lo tanto incognoscible para el grado de precisión requerido por la ciencia moderna. De hecho la esencia y la presencia de un factor en un grado dado no puede utilizarce para predecir, linealmente, el comportamiento de un sistema tales como aves, átomos, moléculas, fotones, personas, especies, o sociedades. Ya no podemos usar la teoría axiomática formal en cojunción con la lógica binaria para modelar la realidad, predecir, y, por lo tanto, controlar la dinámica del sistema. De hecho el control en sí mismo se convierte en una víctima de la ciencia postmoderna. En un ensayo sobre la inutilidad de la institución cada vez mayor de controles en una sociedad se muestra como esta se bifurca en ricos y pobres, en los que tienen y los que no tienen. Si algo nos ha enseñado nuestro sistema penitenciario es que el uso de la policía y un aumento del sistema de justicia penal no ayuda con el problema del orden.

Aún menos seremos capaces de usar gran teoría axiomática como un fundamento sobre el cual producir una política social. Ya no podemos suponer que si algo existe entonces se puede medir con precisión y predecir completamente. Ahora debemos aceptar que, en economía, política, cognición humana, delincuencia, enfermedades, y otros fenómenos naturales, la causalidad abre y cierra, viene y va, se desvanece y reaparece como la sonrisa del gato de Cheshire, en una cuenca de un fractal de eventos. Hay un ensayo sobre Teoría de paradigma junto con fundamentos de ciencia postmoderna los cuales se enfocan mucho más sobre los peculiares saltos, giros, vueltas, y el deambular que toman los hilos de causalidad en la ciencia postmoderna.

En el anverso de dicha capacidad, la incapacidad de conocer completa, perfecta y precisamente ; está una imposibilidad para las variadas culpas, desde la perfección y predicción hasta problemas técnicos, fantasmas, demonios, genes, desviaciones, errores, pecados, agitadores externos, o incompetencia humana. Las interacciones no lineales y bifurcaciones no lineales son atributos comunes de los sistemas sociales y naturales. Lo normal, lo ideal y lo perfecto son vestigios de deseos por conocer todo por parte de científicos, de controlar todo por parte de los administradores, de los burócratas de planificar todo, y de los contadores de categorizar todo. La ciencia postmoderna basada en la Teoría del Caos no sirve en absoluto a las políticas que buscan predecir y controlar todo.


Revisar el ensayo íntegro (en inglés) <---

6to Congreso Latinoamericano de Dinámica de Sistemas

Llamado a presentar trabajos

El Capítulo Latinoamericano de la Sociedad de Dinámica de Sistemas tiene el honor de anunciar su Sexto Congreso Latinoamericano de Dinámica de Sistemas, a realizarse del 22 al 25 Octubre de 2008 en Santiago de Chile. Invitamos a los académicos y los profesionales de la disciplina y de disciplinas relacionadas con el modelamiento y la simulación de sistemas con retroalimentación, a presentar sus trabajos.

Objetivos

El congreso permite a los académicos, profesionales y estudiantes de la dinámica de sistemas de discutir aplicaciones y avances. También les la oportunidad para tomadores de decisión, consultores, académicos y estudiantes de diversos ámbitos de los negocios, del gobierno y de las ciencias sociales y naturales, de establecer contacto con la dinámica de sistemas y sus protagonistas.

Programa

El congreso consiste de un simposio acerca de los sistemas complejos y dinámicos, de sesiones plenarias y paralelas, así como sesiones de poster cubriendo una amplia variedad de ámbitos de aplicación en

• Políticas pública
  • Energía
  • Educación
  • Salud
  • Seguridad ciudadana y criminalidad
  • Desarrollo económico y social
• Gestión y desarrollo empresarial
  • Estrategia empresarial
  • Gestión de cambio
  • Gestión de proyectos
  • Logística
• Medio ambiente
• Educación
• Metodología

Sumisión de trabajos

Aceptamos dos tipos de trabajos:

1. Artículos en extenso
2. Posters con resumen extendido.

Acerca de los artículos en extenso

Los artículos en extenso serán sometidos a revisión anónima por parte de dos árbitros y que – de ser aceptados – serán publicados en las Actas del Congreso. Los revisores pueden recomendar la publicación en el número especial de la Revista de Dinámica de Sistemas.

Los trabajos deben ser redactados en español, portugués o inglés. Todo trabajo sometido requiere un presentador principal inscrito hasta una fecha límite; trabajos sin este respaldo se eliminarán del programa.

Para los artículos que reportan de trabajos de modelamiento, es altamente deseable agregar el modelo o, en su defecto, las ecuaciones como material adicional. Los mejores artículos serán considerados para su publicación en la revista de Dinámica de Sistemas.

Acerca de los posters con resumen extendido

Los posters con resumen extendido son una modalidad especial para autores que no podrán asistir al congreso. Los resúmenes extendidos (4 páginas) serán sometidos a la evaluación del comité de programa y expuestos como posters durante el Congreso, pero no publicados en sus Actas, donde solamente se incluirá el listado de autores de “poster”. Los “posters” se encontrarán en determinadas zonas visibles durante la extensión del congreso. Para esta modalidad rige la tarifa especial de US$20.

Comité delPrograma

Martin Schaffernicht, Universidad de Talca
martin@utalca.cl

Martín Kunc, Universidad Adolfo Ibañez
martin.kunc@uai.cl

Juan Pablo Torres, Universidad Diego Portales
jpablo.torres@udp.cl

Organizan

>>>>>>>>>>>MÁS INFORMACIÓN AQUÍ<<<<<<<<<<<<<

Conocimiento vs Información

Tomado del blog de Extreme Productivity by Design de Skip Walter

Un primer acercamiento a esta cuestión que suele ser un tanto confusa nos lleva a definiciones básicas de ambos términos. Desde un primer repaso diremos que información son datos estructurados y que conocimiento es información en acción. Pero vayamos un poco más lejos. Si recordamos las jerarquías (WUKID: Windsom Sabiduría, Understanding Entendimiento, Knowledge Conocimiento, Information Información, Data Dato) de Russell Ackoff:

• Dato: Es una observación primaria del mundo. Podría ser unalectura de temperatura de 28º, o el precio de un libro , o cualquiera de las cosas observables que nos encontramos cada día.


• Información: Proporciona la estructura para los datos. Un reporte del clima pone la temperatura (dato) en un contexto. La temperatura del aire en Lima PE, fue de 28º el 28 de Julio del 2007, a las 2pm el sol brillaba. Cada uno de los componentes de la oración anterior son datos puestos juntos para formar una información global.


• Conocimiento: Es información procesable. Dada la cadena de información del clima antes mencionada, yopodría saber si habrá un buen día o fresco y en qué momento del año, entonces yo podría usar una camisa ligera y una chaqueta si fuera a salir.


• Entendimiento: Es ver patrones en el conocimiento y la información. Si la cadena de clima antes mencionada se combinara con 20 o 30 días de la misma cadena de información y yo hubiera vivido en Lima por más de 10 años yo sería capaz de ver el patrón de un verano fresco. El entendimiento tiene un componente de tiempo mayor que el de la información y el conocimiento. El entendimieno incorpora un doble bucle de aprnizaje como menciona Schon en su libro The Reflective Practitioner.


• Sabiduría: Es ir más allá de los niveles de entendimiento para ver lo sistemas a gran escala y ser capaz de predecir comportamientos y resultados en un futuro de términos más amplios (5-15 años) basado en los mimo patrones que surgieron del entendimiento. Cuando muchos datos sobre muchos años fueron refinados en información, conocomiento y patrones de entendimiento, los científicos fueron capaces de ver los patrones de clima en el largo plazo como con El Niño y La Niña. Basado en estos patrones de clima los futurólogos del clima pueden predecir tendencias en términos má largos en Lima y actuar de acuerdo a ello.

Elizabeth Orna en Making Knowledge Visible: Communicating Knowledge Through Information Products describe el proceso mediante el cual la información se transforma en conocimiento y viceversa. Afirma que la información vive en el exterior, conde se hace visible y disponible para los otros y es capaz de alimentar su conocimiento, pero el conocimiento no es algo que yo pueda dar a otra persona, porque la información tiene que ser transformada en algo que sólo vive en la mente humana. En general estamos invisible y constantemente transformando información en conocimiento y de nuevo en información para que otros la puedan consumir. El diagrama de esta transformación según Orna se puede ver en el slide 2 de una presentación que di en el Instituto de verano de KM.

Lackoff y Johnson en Metaphors We Live By y Philosophy in the Flesh fueron más allá en sus distinciones entre información y conocimiento reclamando que el conocimiento solo resulta cuando tenemos un cuerpo físico que puede sentir y actuar en el mundo.

Aquí algunos links adicionales

• Nihil Sharma's The Origin of the "Data Information Knowledge Wisdom" Hierarchy"
• Brian Berliner's Brain blog on Learning: Data, Information, Knowledge, Understanding, Wisdom
• Systems Thinking website on Data, Information, Knowledge and Wisdom
• Double Loop Learning from a Wikipedia article on Organizationl Learnin

Encuentro de Sistemas Complejos

Encuentro de Sistemas Complejos

Applicattion of Complex Systems Methods in Engineering

Valparaiso, Chile

14 al 16 de Enero 2008

Los sistemas complejos, desde la célula hasta la ecoesfera, resultan de procesos de evolución y de adaptación. Presentan propiedades emergentes: el nivel microscópico subyacente hace emerger formas organizadas en el nivel macroscópico. Este, a su vez, influencia hacia el nivel microscópico. Las propiedades emergentes son robustas y se pueden estudiar desde diferentes puntos de vista. Ello depende de la clase de sistemas adaptativos complejos que se considere.

El aporte de las disciplinas formales para la modelación de sistemas complejos, ya sean naturales o artificiales, es considerable. ¿Qué sería de la modelación de sistemas complejos sin las transiciones de fase, la renormalización, los estados críticos auto- organizados de la física estadística, sin los sistemas dinámicos de la matemática, sin los sistemas discretos o los autómatas celulares y sin la informática?

La comprensión de los sistemas adaptativos complejos pasa necesariamente por su modelación. Algunos modelos quedan doblemente restringidos, según las reglas habituales de la ciencia: por un lado, deben ser lo más parsimonioso posible, con un contenido teórico inteligible; por el otro, deben permitir la reconstrucción del conjunto de datos que provienen de la observación de esos sistemas. La novedad, sin embargo, proviene de la cantidad de datos acumulados sobre los sistemas complejos, que hoy conoce una expansión muy rápida. No sólo bajo la forma de datos numéricos en patrones 1D, sino también de imágenes 2D y 3D. En ese flujo creciente de datos, la cuestión es detectar los patrones espacio- temporales a ser sometidos a las reconstrucciones racionales de la modelación y de la simulación. Dicha reconstrucción pone en acción métodos inductivos cada vez más sofisticados, con el apoyo de medios computacionales cada vez más poderosos. La actividad de reconstruir datos es, por naturaleza, interdisciplinaria. Ella permite asociar directamente cada disciplina con los especialistas provenientes de las disciplinas formales: matemáticas, informática y física.

Es justamente, en este ir y venir entre la adquisición de datos sobre la base de hipótesis modeladoras y su reconstrucción por medio de la modelación, que una ciencia de los sistemas complejos puede desarrollarse. Los sistemas complejos son objetos esencialmente pluridisciplinarios. Para un mismo objeto, hay teorías diferentes y heterogéneas de las cuales pueden dar cuenta: las actividades neuronales pueden pensarse, a la vez, como ecuaciones dinámicas y como estructura lógica para un determinado contenido.Queda aún mucho por hacer en el plano teórico-sobre la base de lo realizado en el siglo XX- de modo de tener conceptos y modelos que provean explicaciones elegantes a los fenómenos emergentes.

Objetivos

• Presentacion de la Sociedad de Sistemas Complejos (SC).
• Identificar áreas de trabajo conjunto, crear posibles equipos de colaboracion cientifica, analizar posibles acuerdos y proyectos en el area de los sistemas complejos y sus aplicaciones.
• Estudio para una propuesta de curso permanente y transversal de SC en los postgrados de Facultad de ciencias

Workshops

I Reconstruccion de dinamicas de comunidades cientificas: un ejemplo de la cognicion social

1. David Chavalarias :vice presidente de la Sociedad de Sistemas Complejos. Phd en ciencias cognitivas, CREA Ecole Polytechnique. Post-doctorado en sistemas complejos.
2. Jean phillipe Cointet :Phd student en sistemas complejos, CREA Ecole Polytechnique y TSV-INRA.
3. Carla Taramasco :responsable del comite "acciones en latino america" de la Sociedad de Sistemas Complejos. Phd student en sistemas complejos CREA Ecole Polytechnique.

II Desde los pixeles hasta los campos morfo- genéticos: Análisis, modelación y aprendizaje sobre embriogénesis

1. Emmanuel Faure: Phd student en ciencias cognitivas y sistemas complejos CREA Ecole Polytechnique.
2. (P) Masatoshi Funabashi: Phd student en matematica CREA Ecole Polytechnique.
3. (P) Miguel Luengo : Phd Student en ingenieria Universidad Politecnica de Madrid.

Por confirmar (P)

Las propiedades Emergentes

Tomado de NECSI (por Yaneer Bar-Yam) (versión original, en inglés aquí)

EMERGENCIA

Emergencia es...

1. ...Lo que juntas hacen las partes de un sistema y que ellas no podrían hacer por sí mismas: comportamiento colectivo.

2. ...Lo que un sistema hace en virtud de su relación con su medio ambiente, y que este no podría hacer por sí mismo: ejm. su función.

3. ... El acto o proceso de convertirse en un sistema emergente.

De acuerdo con (1) emergencia se refiere al entendimiento de cómo las propiedades colectivas surgen de las propiedades de las partes. En general se refiere a como el comportamiento a gran escala de los sistemas proviene de lo detalles de su estructura, comportamiento y relaciones en una escala menor. En el extremo es cómo el comportamiento macroscópico proviene del comportamiento microscópico.

De acuerdo a esta visión, cuando pensamos en emergencia nosotros estamos, a los ojos de nuestra mente, moviéndonos entre diferentes puntos de vista, Vemos los árboles y el bosque al mismo tiempo. Vemos el modo en que los árboles y el bosque están relacionados el uno con el otro. Para ve en ambos puntos de vista tenemos que ser capaces de ver los detalles, pero además ignorar los detalles. El truco está en saber cuáles de los muchos detalles que vemos en los árboles son importantes para saber cuando estamos viendo el bosque.

La visión del observador convencional considera o los árboles o el bosque. Quienes sólo consideran los árboles consideran que los detalles son lo esencial y no ven los patrones que que surgen cuando consideramos los árboles en el contexto del bosque. Quienes consideran al bosque no ven los detalles. Cuando uno se puede desplazar hacia adelante y hacia atrás entre la vista de los árboles y el bosque uno puede además ver que aspectos de los árboles son relevantes para la descripción del bosque. El entendiendo de esta relación, en general, es el estudio de la emergencia.

Un ejemplo útil es una llave. Una llave tiene una estructura particular. Para describir su estructura no es suficiente decirle a alguien que esta puede abrir una puerta. Nosotros tenemos que saber ambas cosas, la estructura de la llave y de la cerradura. Sin la descripción de la estructura de cualquiera de ellos, sin embargo, podemos decirle a alguien que esta puede destrabar la puerta.

Uno de los problemas en la forma de pensar en los conceptos de sistemas complejos es que a menudo nosotros asignamos propiedades a un sistema que no son si no propiedades de una relación entre el sistema y su entorno. ¿Por qué hacemos esto? Porque nos hace pensar en lo que ocurre de modo más simple. ¿Por qué podemos hacer esto? Porque cuando el entorno no cambia entonces sólo necesitamos describir el sistema y no el entorno para dar la relación. Así, la relación está muchas veces implícita en lo que decimos y pensamos.

El segundo aspecto de emergencia (2) está relacionado al primer aspecto (1) porque el sistema puede ser visto con partes de su entorno así juntos formando un sistema mayor. El comportamiento colectivos debido a las relaciones de las partes del sistema mayor reflejan las relaciones del sistema original con su entorno.

Los roles de las relaciones:

• Ambos (1) y (2) tienen que ver con las relaciones, las relaciones de las partes o las relaciones del sistema a su entorno. Cuando las partes de un sistema están relacionadas a cada una de las otras nosotros hablamos de ellas como una red, cuando un istema esta relacionado a partes de un sistema mayor nosotros hablamos de su ecosistema.

El rol de los patrones:

• Cuando hay relaciones que existen entre las partes de un sistema nosotros hablamos de patrones de comportamiento.

La idea de emergencia es contrastada muchas veces con la perspectiva reduccionista. La perspectiva reduccionista piensa en las partes de manera aislada. Esta es la muchas veces vilipendiada visión del mundo de “sistemas anti-complejos”. Sin embargo, aún la idea de “sistema” esta basada en un reduccionismo parcial. para entender esto uno debería entender cuidadosamente la noción de aproximación o “verdad-parcial” la cual es esencial para el estudio de los sistemas complejos.