... viene de la parte I...
El propósito de este artículo es ilustrar, a través del ejemplo de la dinámica humana, que un entendimiento minucioso de un sistema complejo requiere un entendimiento de la dinámica de la red así como la topología y arquitectura de la red.
Luego de un panorama de la topología de las redes complejas tales como la Internet y la WWW, se dan los modelos generados por datos para dinámicas humanas. Estos modelos motivan el estudio de las dinámicas de las redes y sugieren que la teoría de la complejidad debe incorporar la interacción entre la dinámica y la estructura. El artículo además advierte la noción que un entendimiento de la dinámica de la red es facilitada por la disponibilidad de grandes conjuntos de datos y las herramientas de análisis venidas del estudio de la estructura de la red.
EL PARADIGMA DE LA RED ALEATORIA
Las redes complejas fueron inicialmente pensadas como si fueran completamente aleatorias. Este paradigma tiene sus raíces en los trabajos de Paul Erdös y Alfréd Rényi quienes, ayudando a describir las redes en comunicaciones y ciencias de la vida, sugirieron en 1959 que las redes se modelaran como grafos aleatorios [7], [8]. Este enfoque tomaba N nodos y los conectaba con L vínculos colocados aleatoriamente. La simplicidad del modelo y la elegancia de la teoría permitieron la emergencia de las redes aleatorias como un campo de estudio de las matemáticas [7]-[9].
Una predicción clave de la teoría de las redes aleatorias es que, a pesar de la posición aleatoria de los vínculos, la mayoría de nodos son asignados aproximadamente con el mismo número de vínculos. Ciertamente, en una red aleatoria los nodos siguen la distribución de campana de Poisson. Encontrar nodos que tienen un número significativamente grande o pequeño de vínculos en una elección aleatoria es por lo tanto raro. Las redes aleatorias son también conocidas como redes exponenciales porque la probabilidad de que un nodo esté conectado a otros k nodos decrementa exponencialmente por el tamaño de k (Figura 1). El modelo de Erös-Rényi, sin embargo, plantea la pregunta del si las redes observadas en la naturaleza son aleatorias. ¿Podría el Internet, por ejemplo, ofrecer servicio rápido y sin cortes si las computadoras estuvieran conectadas aleatoriamente unas con otras? ¿O podrías leer este artículo si los químicos en tu cuerpo repentinamente decidieran reaccionar aleatoriamente unos con otros sin pasar por la rígida red química que normalmente obedecen? Intuitivamente la respuesta es no, debido a que suponemos que detrás de cada sistema complejo hay una red subyacente con una topología no aleatoria. El reto del estudio de la estructura de redes, sin embargo, es escarbar en las señales de orden de la colección de millones de nodos y vínculos que forman una red compleja.
LA WORLD WIDE WEB Y LA INTERNET COMO REDES COMPLEJAS
La WWW contiene más de un billón de documentos (páginas web) los cuales representan los nodos de una red compleja. Estos documentos están conectados por un localizador de recursos uniforme (URLs), los cuales son usados para navegar de un documento a otro [Figura 2(a)]. Analizar las propiedades de la WWW, un mapa de cómo las páginas web están conectadas unas a otras se obtuvo en [10] usando un robot, o web crawler, el cual empezó desde una página web dada y recolectó las páginas a las cuales esta vinculaba (link). El robot luego siguió cada link de salida para visitar más páginas, recolectando sus respectivos links [10]. A través de este proceso iterativo una pequeña pero representativa fracción de la WWW puede ser mapeada.
Debido a que la WWW es una red direccionada cada documento está caracterizado por el número kout de sus links de salida, y el número kin de sus links de entrada. La distribución del grado de salida (entrada) por lo tanto representa la probabilidad P(k) de que una web seleccionada aleatoriamente tenga exactamente kout (kin) links. Además la teoría de grafos predice que P(k) sigue la distribución de la ley de potencias mostrada en la figura 2(c) y descrita por:
P(k) ~ k – γ, (1)
Donde γout ≈ 2.45 (γin ≈ 2.1).
Como lo ilustra la Figura 1, mayores diferencias topológicas existen en una red con una distribución de conectividad de Poisson y una con una distribución de conectividad de ley de potencias. De hecho la mayoría de los nodos en una red aleatoria unidireccional tienen aproximadamente el mismo número de links dados por k ≈ (k), donde el grado promedio. El decaimiento exponencial de la distribución de Poisson P(k) garantiza la ausencia de nodos con una significativa cantidad de nodos mayores que k y por ello impone una escala natural en la red. En cambio la distribución de ley de potencias implica que nodos con pocos links son abundantes mientras un pequeño número de nodos tienen abundantes links. Un mapa del sistema de carreteras de los EEUU, donde las ciudades son nodos y las autopistas son vínculos, ilustran una red exponencial. La mayoría de ciudades se ubican en la intersección de dos a cinco autopistas. Por otro lado, una red de escala libre es similar a los mapas de rutas de avión que se muestran en los folletos de vuelos. Mientras la mayoría de aeropuertos son alimentados por unos pocos transportistas, unos pocos hubs, tales como Chicago o Frankfurt, tienen enlaces a casi todos los aeropuertos en EEUU y Europa respectivamente. De este modo, al igual que los aeropuertos más pequeños, la mayoría de documentos WWW tienen un pequeño número de links, y , si bien estos links no son suficientes por sí mismos para garantizar que la red esté totalmente conectada, los pocos altamente conectados hubs garantizan que la WWW se mantenga unida.
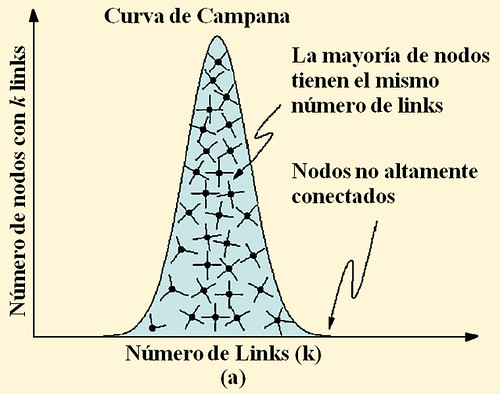

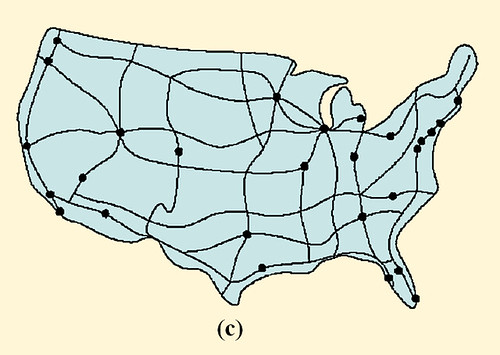
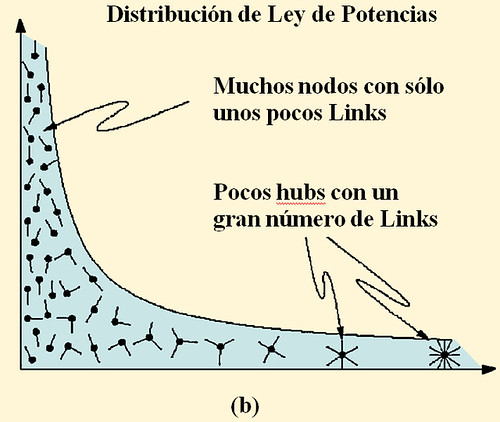
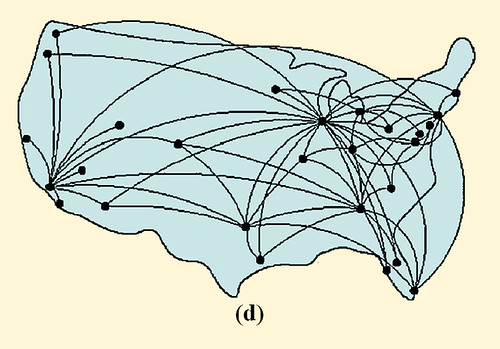
FIGURA 1 Redes Aleatorias y de escala libre. El grado de distribución de una red aleatoria sigue la distribución de Poisson cerrada con la forma de una curva de campana, diciéndonos que casi todos los nodos tienen el mismo número de links, y que los nodos con un gran número de links no existen (a). Esto es, una red aleatoria es similar a una red nacional de carreteras en las cuales los nodos son as ciudades y los vínculos son las mayores carreteras que las conectan. De hecho la mayoría de ciudades son conectadas por aproximadamente el mismo número de carreteras (c). en cambio la distribución de grado de ley de potencias de una red de escala libre predice que la mayoría de nodos tienen sólo unos pocos links que se mantienen juntos por muy pocos hubs altamente conectados (b). Tal red es similar al sistema de tráfico aéreo, en el cual un gran número de pequeños aeropuertos están conectados unos a otros mediante unos pocos hubs mayores (d). Luego [1]
A diferencia de la distribución de Poisson, una distribución de ley de potencias no posee una escala intrínseca, y su grado promedio
La topología de escala libre de la WWW motiva la búsqueda de topologías no homogéneas en otros sistemas complejos tales como el Internet. Así como la WWW, el Internet es una red física cuyos nodos son routers y dominios y cuyos vínculos son líneas telefónicas y cables de fibra óptica que conectan los nodos [Figura 2(b)]. Debido a su naturaleza física, se espera que el Internet sea estructuralmente diferente a la WWW, dónde añadir un link arbitrariamente a una página web remota es tan fácil como linkear una página web en una computadora en la habitación del costado. La red Internet, sin embargo, además parece seguir el grado de distribución de ley de potencias como se observa en [12] [Ver Figura 2(b)]. En particular el grado de distribución mostrado sigue una ley de potencias con exponente y=2.5 para el router de la red, y y=2.2 para el mapa de dominio, lo cual indica que el cableado del Internet está además dominado por muchos hubs altamente conectados [12].
19 Grados de Separación
Stanley Milgram mostró empíricamente en 1967 que dos personas cualesquiera están de 5 a seis “apretones de mano” alejados uno del otro. [13]. Esto es, la mayoría de humanos en la tierra parecen vivir en un pequeño mundo. Esta característica de las redes sociales es conocida como propiedad de los seis grados de separación (six-degrees of separation) [14]. Además los sociólogos sostienen repetidamente que los nodos en las redes sociales están agrupados en pequeños clusters. Estos clusters representan círculos de amigos y conocidos, y dentro de cada cluster un nodo está conectado a todos los otros nodos pero tiene sólo escasos vínculo con el mundo exterior [15]. La pregunta que surge es si el modelo del mundo pequeño es aplicable a la WWW y al Internet.
Debido a que no hay disponible un mapa completo de la WWW [16], se usan pequeños modelos de computadora de la WWW en [10], donde la distribución del vínculo coincide con la forma de medición funcional y donde las distancias más cortas entre cualesquiera dos nodos son identificados y promediados para todos los pares de nodos para obtener la separación promedio de nodos d. Repitiendo este proceso para redes de diferentes tamaños usando escalamiento de tamaño finito, un procedimiento estándar en mecánica estadística, se infiere en [10] que d=0.35+2.06.Log(N), donde N es el número de nodos de la WWW. Para los 800 millones de nodos de la WWW en 1999, el típico camino más corto entre dos páginas web aleatoriamente seleccionadas es pues alrededor de 19, asumiendo que cada camino existe, lo cual no está siempre garantizado debido a la naturaleza direccionada de la web. Como se muestra de forma empírica en [17], sin embargo, para 200 millones de nodos esta distancia es 16, en contraste con los 17 predichos en [10].
Estos resultados indican que la WWW representa un pequeño mundo y que el número típico de clicks entre dos páginas web es alrededor de 19, a pesar del número actual de más de 1 billón de páginas web. Además, la WWW muestra un alto grado de clustering [18], esto es, la probabilidad que dos vecinos de un nodo dado estén también linkeados es mucho mayor que el valor esperado para una red aleatoria. Finalmente, los resultados del reporte en [1] indican que el Internet además posee una estructura de pequeño mundo.
3 comentarios:
Se dice "campana de Gauss".
La verdad es que aportas con tu blog y coincido en muchas de tus películas favoritas y algunos grupos, sobre todo, en Francoise Hardy (aunque parezca dispar).
Programé el Z80 y manejaba el DOS 2.1 en BASIC y LOGO. No soy gay.
Me alegra ver gente como tú. Aprobé filosofía en septiembre y me alegro que Nietzche muriese de "reblandecimiento del cerebro".
Bixen...Gracias por la nota al pie, efectivamente la curva de campana es también conocida como Campana de Gauss (de Gauss-Laplace en algunos textos de estadística).
Este fin de semana posteo la tercera parte de la traducción de este artículo de Barabasi
Veo que sabes que el Z80 no era de Intel. Leeré el artículo. Gracias!
Publicar un comentario